Parallele Programmierung - MPI

Einführung

MPI bedeutet Message Passing Interface. Es ist eine Bibliothek, die man in C/C++ und Fortran-Programmen benutzen kann. Wie der Name schon sagt, ist MPI ein System zur Übertragung von Nachrichten auf Multiprozessorsystemen wie z. B. unserem Cluster. Es wurde 1993-94 von einer Gruppe aus Wissenschaft und Industrie entwickelt.

Vorgehensweise

Zuerst muss die Bibliothek mittels #include <mpi.h> eingefügt werden.

MPI besteht aus 125 Funktionen. Die wichtigsten für den Anfang werden hier genannt und erklärt:

MPI_Init(&argc,&argv) ist die Initialisierungsroutine. Sie muss vor dem Benutzen von MPI-Befehlen ausgeführt werden. Die Argumente lauten argc und argv und sind Pointer auf Parameter der Hauptfunktion.
MPI_Finalize() beendet MPI und räumt sämtlichen hinterlassenen Müll von MPI weg.
MPI_Abort() sorgt für einen sauberen Abbruch im Fehlerfall.
MPI_Comm_Size(MPI_Comm comm, int size) gibt die Anzahl der beteiligten Prozesse durch das zweite Argument (size) zurück. Das erste Argument ist ein Kommunikator. Letztenendes ist das eine Anzahl von Prozessen, die Nachrichten austauschen. Für einfache Programme wird jedoch nur
MPI_Comm_World benötigt. Dies beinhaltet alle Prozesse, die laufen, wenn die Ausführung beginnt (siehe auch Kommunikationsarten).
MPI_Comm_Rank(MPI_Comm comm, int rank) gibt den Rang (Prozessidentifikation) zurück.

Zentrale Send-/Receive-Funktionen:

MPI_Send(start, count, datatype, dest, tag, comm) Standardfunktion zum Senden von Nachrichten. Start bestimmt die Speicheradresse, count die Länge und Datatype den Datentyp (hier immer MPI-Datentypen, keine C- oder Fortran-Datentypen). Tags sind zur Bestimmung von Kontexten, z.B. wenn zwei Nachrichten zwei floats senden, die einmal verarbeitet und einmal gedruckt werden sollen. Dest (Send) und Source (Receive) sind die Ränge der sendenden oder empfangenden Prozesse. MPY_ANY_SOURCE ist eine Wildcard für source, wenn man von irgendeinem Prozess statt eines speziellen empfangen will.
MPI_Recv(start, count, datatype, source, tag, comm, status) Standardfunktion zum Empfang von Nachrichten.
MPI_Bcast(start, count, datatype, source, tag, comm, status) sendet von einem an alle Knoten.
MPI_Reduce(start, result, count, datatype, operation, root, comm) sammelt Daten von allen Knoten mittels einer bestimmten Operation(MPI_MAX, MPI_MIN, MPI_SUM, MPI_PROD, MPI_LAND, MPI_BAND, MPI_LOR, MPI_BOR, MPI_LXOR, MPI_BXOR, MPI_MAXLOC, MPI_MINLOC; die letzen zwei suchen auch noch den Ort).

Aufgabenstellung Übungsblatt 2

Das Integral einer stetigen Funktion kann als Fläche gedeutet werden. An der Bestimmung der Fläche unter der durch den Integranden bestimmten Funktion über einem Intervall [a, b] ist man in vielen praktischen Anwendungen interessiert. Falls die Stammfunktion F des Integranden f formelmäßig bestimmt werden kann, gilt

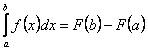
Die numerische Auswertung eines bestimmten Integrals kann allerdings häufig nur näherungsweise erfolgen, denn für viele Integrale lässt sich die Stammfunktion nur mit viel Aufwand oder sogar überhaupt nicht formelmäßig bestimmen.

Gegenüber der Rechteckregel und Trapezregel lässt sich eine wesentliche Verbesserung erzielen, wenn die Intervallenden nicht durch eine Gerade, sondern durch Parabelbögen verbunden werden. Dies bringt eine wesentlich bessere Näherung, so dass deutlich weniger Rechenschritte für ein genaues Resultat benötigt werden. Diese Integrationsregel beruht auf der sogenannten keplerschen Fassregel, die vom bekannten Astronomen Johannes Kepler (1571-1630) vorgestellt wurde, um die Fläche eines solchen fassförmigen Flächenelementes näherungsweise zu bestimmen. 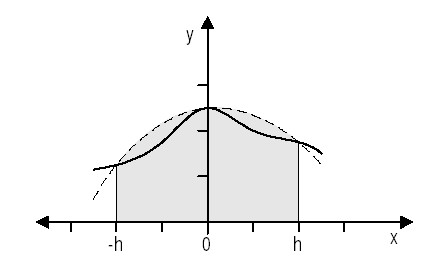Der sonst nicht weiter bekannte englische Mathematiker Thomas Simpson (1710-1761) benutzte diese Formel um den Integralwert mit n Teilflächen zu berechnen.

Abbildung 1 — Kepler’sche Fassregel

Die Näherungsfläche wird als Parabelbogen, der durch die Punkte f(-h), f(0) und f(h) geht, gelegt. Für das Integral ergibt sich damit die folgende Näherungsformel:

Berechnen sie die Näherungsfläche mit Hilfe des Simpsonverfahrens einer von Ihnen beliebig (einstellbaren) gewählten Funktion (z.B. y=sin(x)) in einem einstellbaren Intervall (z.B. [0, p]) mittels MPI auf den Rechnern {sgi-itec,pl01-itec,pl02-itec,pl03-itec}.uni-klu.ac.at.

ssh-Konfiguration:

· Generierung eines Authentifizierungsschlüssels (auf der sgi-itec) mittels ssh-keygen -t type wobei type={rsa1, rsa} ist. Dies legt folgende Dateien im ~/.ssh-Verzeichnis an

o id_rsa

o id_rsa.pub

o identity

o identity.pub

Den Inhalt von den *.pub-Dateien wird nun auf die anderen Rechnern in die authorized_keys-Datei übertragen.

Testen der ssh-Konfiguration mittels MPI-Beispielprogramm:

netarc00@sgi-itec:~> mpirun -np 4 /usr/local/mpi/examples/cpi

Process 0 on sgi-itec.uni-klu.ac.at

Process 3 on pl03-itec.uni-klu.ac.at

Process 2 on pl02-itec.uni-klu.ac.at

Process 1 on pl01-itec.uni-klu.ac.at

pi is approximately 3.1416009869231245, Error is 0.0000083333333314

wall clock time = 0.002840

Termine:

Abgabe des Quellcodes per Email bis 07.05.2003
Präsentation der Ergebnisse am 08.05.2003

Fragen:

· Tel.: +43/463/2700 3621

· Email: christian.timmerer@itec.uni-klu.ac.at